Long Working Distance Objectives

- Objectives for UV, Visible, or NIR Light
- 5X, 7.5X, 10X, 20X, 50X, or 100X Magnification
- Ideal for Machine Vision Applications
- Infinity-Corrected Design
MY5X-822
5X Objective
480 nm - 1800 nm
MY100X-806
100X Objective
436 nm - 656 nm
HPA50XAB
50X Objective
400 nm - 1100 nm
LMUL-10X-UVB
10X Objective
240 nm - 360 nm

Please Wait
| Objective Lens Selection Guide |
|---|
| Objectives |
| Thorlabs Microscopy Objectives for Life Sciences Imaging Microscopy Objectives Microscopy Objectives, Oil Immersion Physiology Objectives, Water Dipping or Immersion Phase Contrast Objectives Long Working Distance Objectives Reflective Microscopy Objectives UV Focusing Objectives VIS and NIR Focusing Objectives |
| Scan Lenses and Tube Lenses |
| Scan Lenses F-Theta Scan Lenses Infinity-Corrected Tube Lenses |
| Click on the red Document icon next to the item numbers below to access the Zemax file download. Our entire Zemax Catalog is also available. |
Click for Details
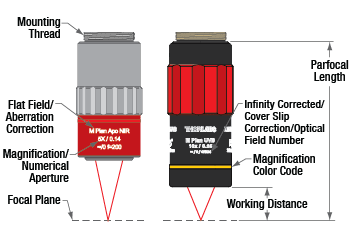
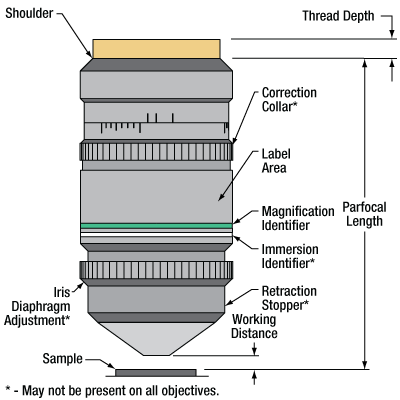
Figure 1.1 This diagram illustrates the labels, working distance, and parfocal distance. The format of the engraved specifications will vary between objectives and manufacturers. (See the Objective Tutorial tab for more information about microscope objective types.)
Features
- Long Working Distance Ideal for Machine Vision Applications
- Infinity-Corrected Options for UV, Visible, or NIR Wavelengths
- Designed for a Tube Lens Focal Length of 200 mm
- W26* x 0.706 Threading
Thorlabs offers long working distance M Plan objectives for ultraviolet (UV), visible, or near-infrared (NIR) wavelength ranges. These objectives are designed for use with a tube lens focal length of 200 mm and are ideal for machine vision applications or applications that require a significant distance between the objective lens and the object. See the Specs tab for details on each of the objectives available here.
Each objective housing is engraved with key specifications including the magnification, the numerical aperture, and an infinity symbol noting that it is infinity corrected; see Figure 1.1. The housings have external W26 x 0.706 threads.
All of the objectives found on this page have a parfocal length of 95 mm (see the Specs tab for complete specifications). To use them alongside other manufacturer standards, such as Nikon objectives with a 60 mm parfocal length, we offer parfocal length extenders. For instance, the PLE351 Extender can be used to increase the parfocal length of a Nikon objective from 60 mm to 95 mm. The W26 x 0.706-threaded objectives featured on this page require an RMSW26S or M25W26S microscope objective thread adapter for compatibility with our parfocal length extenders; note that the use of an adapter could increase the parfocal length.
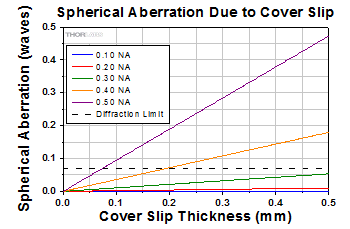
These objectives are designed to be used without a cover glass and do not feature a correction collar. Imaging through a cover glass may cause spherical aberrations in an image, depending on the numerical aperture of the objective. See the Objective Tutorial tab for more on how a cover glass may impact performance. For biological applications where imaging through cover glasses is required, consider our apochromatic objectives for life science.
*Please note that W26-threaded objectives are sometimes labeled as M26-threaded. As long as the objective conforms to ISO 9345:2019 or JIS B 7141:2012, it is considered to have W26 threads.
| Item # | AR Coating Wavelength Range |
Ma | WD | EFL | NA | EPb | Resolutionc | Performance Graphs | OFN | PFLd | Design Tube Lens Focal Lengthe | AR Coating Reflectance |
Pulsed Damage Threshold |
Objective Threading |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Thorlabs Long Working Distance, Achromatic, MicroSpot® UV Focusing Objectives | ||||||||||||||
| LMUL-10X-UVB | 240 - 360 nm | 10X | 20.0 mm | 20 mm | 0.25 | 10.0 mm | 0.9 µm | Raw Data |
24 | 95.0 mm | 200 mm | (240 - 360 nm)f |
5.0 J/cm2 (355 nm, 10 ns, 20 Hz, Ø0.342 mm) |
W26 x 0.706; 5 mm Depth |
| LMUL-20X-UVB | 20X | 15.3 mm | 10 mm | 0.36 | 7.2 mm | 0.6 µm | Raw Data |
|||||||
| LMUL-50X-UVB | 50X | 12.0 mm | 4 mm | 0.42 | 3.4 mm | 0.5 µm | Raw Data |
|||||||
| Thorlabs High Resolution VIS+ Plan Apochromatic Objectives | ||||||||||||||
| HPA50XAB | 400 - 1100 nm | 50X | 5.0 mm | 4 mm | 0.75 | 6.0 mm | 0.4 µm | 24 | 95.0 mm | 200 mm | Ravg < 1.0% (400 - 1100 nm)f |
1.0 J/cm2 (532 nm, 10 ns, 10 Hz, Ø0.408 mm) |
W26 x 0.706; 5 mm Depth |
|
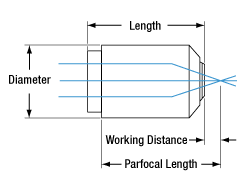
Figure 2.1 Dimensional Drawing of a
Microscope Objective

Figure 2.2 Dimensional Drawing of a
Microscope Objective
| Table 89A Chromatic Aberration Correction per ISO Standard 19012-2 | ||
|---|---|---|
| Objective Class | Common Abbreviations | Axial Focal Shift Tolerancesa |
| Achromat | ACH, ACHRO, ACHROMAT | |δC' - δF'| ≤ 2 x δob |
| Semiapochromat (or Fluorite) |
SEMIAPO, FL, FLU | |δC' - δF'| ≤ 2 x δob |δF' - δe| ≤ 2.5 x δob |δC' - δe| ≤ 2.5 x δob |
| Apochromat | APO | |δC' - δF'| ≤ 2 x δob |δF' - δe| ≤ δob |δC' - δe| ≤ δob |
| Super Apochromat | SAPO | See Footnote b |
| Improved Visible Apochromat | VIS+ | See Footnotes b and c |
Parts of a Microscope Objective
Click on each label for more details.
Figure 89C This microscope objective serves only as an example. The features noted above with an asterisk may not be present on all objectives; they may be added, relocated, or removed from objectives based on the part's needs and intended application space.
Objective Tutorial
This tutorial describes features and markings of objectives and what they tell users about an objective's performance.
Objective Class and Aberration Correction
Objectives are commonly divided by their class. An objective's class creates a shorthand for users to know how the objective is corrected for imaging aberrations. There are two types of aberration corrections that are specified by objective class: field curvature and chromatic aberration.
Field curvature (or Petzval curvature) describes the case where an objective's plane of focus is a curved spherical surface. This aberration makes widefield imaging or laser scanning difficult, as the corners of an image will fall out of focus when focusing on the center. If an objective's class begins with "Plan", it will be corrected to have a flat plane of focus.
Images can also exhibit chromatic aberrations, where colors originating from one point are not focused to a single point. To strike a balance between an objective's performance and the complexity of its design, some objectives are corrected for these aberrations at a finite number of target wavelengths.
Five objective classes are shown in Table 89A; only three common objective classes are defined under the International Organization for Standards ISO 19012-2: Microscopes -- Designation of Microscope Objectives -- Chromatic Correction. Due to the need for better performance, we have added two additional classes that are not defined in the ISO classes.
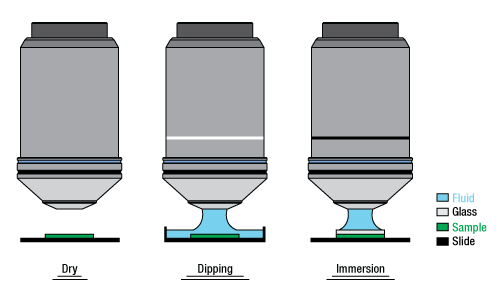
Immersion Methods
Click on each image for more details.
Figure 89B Objectives can be divided by what medium they are designed to image through. Dry objectives are used in air; whereas dipping and immersion objectives are designed to operate with a fluid between the objective and the front element of the sample.
| Glossary of Terms | |
|---|---|
| Back Focal Length and Infinity Correction | The back focal length defines the location of the intermediate image plane. Most modern objectives will have this plane at infinity, known as infinity correction, and will signify this with an infinity symbol (∞). Infinity-corrected objectives are designed to be used with a tube lens between the objective and eyepiece. Along with increasing intercompatibility between microscope systems, having this infinity-corrected space between the objective and tube lens allows for additional modules (like beamsplitters, filters, or parfocal length extenders) to be placed in the beam path. Note that older objectives and some specialty objectives may have been designed with finite back focal lengths. In their inception, finite back focal length objectives were meant to interface directly with the objective's eyepiece. |
| Entrance Pupil Diameter (EP) | The entrance pupil diameter (EP), sometimes referred to as the entrance aperture diameter, corresponds to the appropriate beam diameter one should use to allow the objective to function properly. EP = 2 × NA × Effective Focal Length |
| Field Number (FN) and Field of View (FOV) |
The field number corresponds to the diameter of the field of view in object space (in millimeters) multiplied by the objective's magnification. Field Number = Field of View Diameter × Magnification |
| Magnification (M) | The magnification (M) of an objective is the lens tube focal length (L) divided by the objective's effective focal length (F). Effective focal length is sometimes abbreviated EFL: M = L / EFL . The total magnification of the system is the magnification of the objective multiplied by the magnification of the eyepiece or camera tube. The specified magnification on the microscope objective housing is accurate as long as the objective is used with a compatible tube lens focal length. Objectives will have a colored ring around their body to signify their magnification. This is fairly consistent across manufacturers; see the Parts of a Microscope Objective section for more details. |
| Numerical Aperture (NA) | Numerical aperture, a measure of the acceptance angle of an objective, is a dimensionless quantity. It is commonly expressed as: NA = ni × sinθa where θa is the maximum 1/2 acceptance angle of the objective, and ni is the index of refraction of the immersion medium. This medium is typically air, but may also be water, oil, or other substances. |
| Working Distance (WD) |
The working distance, often abbreviated WD, is the distance between the front element of the objective and the top of the specimen (in the case of objectives that are intended to be used without a cover glass) or top of the cover glass, depending on the design of the objective. The cover glass thickness specification engraved on the objective designates whether a cover glass should be used. |
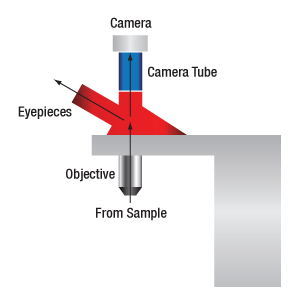
Figure 73A When viewing an image with a camera, the system magnification is the product of the objective and camera tube magnifications. When viewing an image with trinoculars, the system magnification is the product of the objective and eyepiece magnifications.
| Table 73B Focal Lengths by Manufacturer | |
|---|---|
| Manufacturer | Tube Lens Focal Length |
| Leica | f = 200 mm |
| Mitutoyo | f = 200 mm |
| Nikon | f = 200 mm |
| Olympus | f = 180 mm |
| Thorlabs | f = 200 mm |
| Zeiss | f = 165 mm |
Magnification and Sample Area Calculations
Magnification
The magnification of a system is the multiplicative product of the magnification of each optical element in the system. Optical elements that produce magnification include objectives, camera tubes, and trinocular eyepieces, as shown in Figure 73A. It is important to note that the magnification quoted in these products' specifications is usually only valid when all optical elements are made by the same manufacturer. If this is not the case, then the magnification of the system can still be calculated, but an effective objective magnification should be calculated first, as described below.
To adapt the examples shown here to your own microscope, please use our Magnification and FOV Calculator, which is available for download by clicking on the Magnification and FOV Calculator button. Note the calculator is an Excel spreadsheet that uses macros. In order to use the calculator, macros must be enabled. To enable macros, click the "Enable Content" button in the yellow message bar upon opening the file.
Example 1: Camera Magnification
When imaging a sample with a camera, the image is magnified by the objective and the camera tube. If using a 20X Nikon objective and a 0.75X Nikon camera tube, then the image at the camera has 20X × 0.75X = 15X magnification.
Example 2: Trinocular Magnification
When imaging a sample through trinoculars, the image is magnified by the objective and the eyepieces in the trinoculars. If using a 20X Nikon objective and Nikon trinoculars with 10X eyepieces, then the image at the eyepieces has 20X × 10X = 200X magnification. Note that the image at the eyepieces does not pass through the camera tube, as shown by Figure 73A.
Using an Objective with a Microscope from a Different Manufacturer
Magnification is not a fundamental value: it is a derived value, calculated by assuming a specific tube lens focal length. Each microscope manufacturer has adopted a different focal length for their tube lens, as shown by Table 73B. Hence, when combining optical elements from different manufacturers, it is necessary to calculate an effective magnification for the objective, which is then used to calculate the magnification of the system.
The effective magnification of an objective is given by Equation 1:
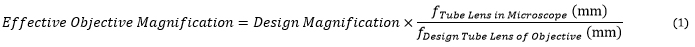
Here, the Design Magnification is the magnification printed on the objective, fTube Lens in Microscope is the focal length of the tube lens in the microscope you are using, and fDesign Tube Lens of Objective is the tube lens focal length that the objective manufacturer used to calculate the Design Magnification. These focal lengths are given by Table 73B.
Note that Leica, Mitutoyo, Nikon, and Thorlabs use the same tube lens focal length; if combining elements from any of these manufacturers, no conversion is needed. Once the effective objective magnification is calculated, the magnification of the system can be calculated as before.
Example 3: Trinocular Magnification (Different Manufacturers)
When imaging a sample through trinoculars, the image is magnified by the objective and the eyepieces in the trinoculars. This example will use a 20X Olympus objective and Nikon trinoculars with 10X eyepieces.
Following Equation 1 and Table 73B, we calculate the effective magnification of an Olympus objective in a Nikon microscope:
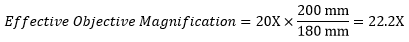
The effective magnification of the Olympus objective is 22.2X and the trinoculars have 10X eyepieces, so the image at the eyepieces has 22.2X × 10X = 222X magnification.
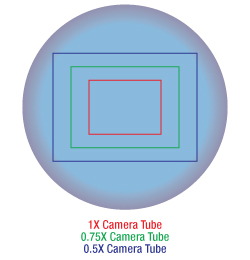 Figure 73C Sample Area When Imaged on a Camera
Figure 73C Sample Area When Imaged on a CameraSample Area When Imaged on a Camera
When imaging a sample with a camera, the dimensions of the sample area are determined by the dimensions of the camera sensor and the system magnification, as shown by Equation 2.
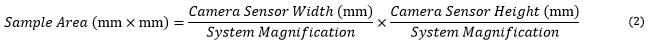
The camera sensor dimensions can be obtained from the manufacturer, while the system magnification is the multiplicative product of the objective magnification and the camera tube magnification (see Example 1). If needed, the objective magnification can be adjusted as shown in Example 3.
As the magnification increases, the resolution improves, but the field of view also decreases. The dependence of the field of view on magnification is shown in Figure 73C.
Example 4: Sample Area
The dimensions of the camera sensor in Thorlabs' previous-generation 1501M-USB Scientific Camera are 8.98 mm × 6.71 mm. If this camera is used with the Nikon objective and trinoculars from Example 1, which have a system magnification of 15X, then the image area is:
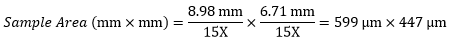
Sample Area Examples
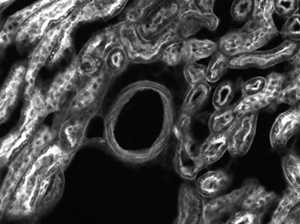
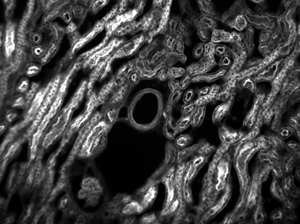
Figures 73D through 73F, images of a mouse kidney, were all acquired using the same objective and the same camera. However, the camera tubes used were different. Figures 73D through 73F demonstrate that decreasing the camera tube magnification enlarges the field of view at the expense of the size of the details in the image.
Resolution Tutorial
An important parameter in many imaging applications is the resolution of the objective. This tutorial describes the different conventions used to define an objective's resolution. Thorlabs provides the theoretical Rayleigh resolution for all of the imaging objectives offered on our site; the other conventions are presented for informational purposes.
Resolution
The resolution of an objective refers to its ability to distinguish closely-spaced features of an object. This is often theoretically quantified by considering an object that consists of two point sources and asking at what minimum separation can these two point sources be resolved. When a point source is imaged, rather than appearing as a singular bright point, it will appear as a broadened intensity profile due to the effects of diffraction. This profile, known as an Airy disk, consists of an intense central peak with surrounding rings of much lesser intensity. The image produced by two point sources in proximity to one another will therefore consist of two overlapping Airy disk profiles, and the resolution of the objective is therefore determined by the minimum spacing at which the two profiles can be uniquely identified. There is no fundamental criterion for establishing what exactly it means for the two profiles to be resolved and, as such, there are a few criteria that are observed in practice. In microscopic imaging applications, the two most commonly used criteria are the Rayleigh and Abbe criteria. A third criterion, more common in astronomical applications, is the Sparrow criterion.
Rayleigh Criterion
The Rayleigh criterion states that two overlapping Airy disk profiles are resolved when the first intensity minimum of one profile coincides with the intensity maximum of the other profile [1]. It can be shown that the first intensity minimum occurs at a radius of 1.22λf/D from the central maximum, where λ is the wavelength of the light, f is the focal length of the objective, and D is the entrance pupil diameter. Thus, in terms of the numerical aperture (NA = 0.5*D/f), the Rayleigh resolution is:
rR = 0.61λ/NA
An idealized image of two Airy disks separated by a distance equal to the Rayleigh resolution is shown in Figure 109A; the illumination source has been assumed to be incoherent. A corresponding horizontal line cut across the intensity maxima is plotted in Figure 109B. The vertical dashed lines in the intensity profile show that the maximum of each individual Airy disk overlaps with the neighboring minimum. Between the two maxima, there is a local minimum which appears in the image as a gray region between the two white peaks.
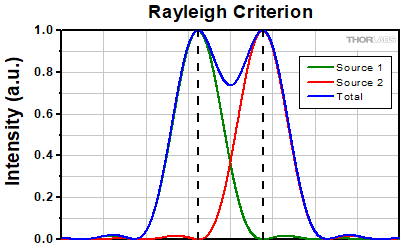 Click to Enlarge
Click to EnlargeFigure 109B The vertical dashed lines show how the maximum of each intensity profile overlaps with the first minimum of the other.
 Figure 109A Two point sources are considered resolved when separated by the Rayleigh resolution. The gray region between the two white peaks is clearly visible.
Figure 109A Two point sources are considered resolved when separated by the Rayleigh resolution. The gray region between the two white peaks is clearly visible.Thorlabs provides the theoretical Rayleigh resolution for all of the imaging objectives offered on our site in their individual product presentations.
Abbe Criterion
The Abbe theory describes image formation as a double process of diffraction [2]. Within this framework, if two features separated by a distance d are to be resolved, at a minimum both the zeroth and first orders of diffraction must be able to pass through the objective's aperture. Since the first order of diffraction appears at the angle: sin(θ1) = λ/d, the minimum object separation, or equivalently the resolution of the objective, is given by d = λ/n*sin(α), where α is the angular semi-aperture of the objective and a factor of n has been inserted to account for the refractive index of the imaging medium. This result overestimates the actual limit by a factor of 2 because both first orders of diffraction are assumed to be accepted by the objective, when in fact only one of the first orders must pass through along with the zeroth order. Dividing the above result by a factor of 2 and using the definition of the numerical aperture (NA = n*sin(α)) gives the famous Abbe resolution limit:
rA = 0.5λ/NA
In Figure 109C, two Airy disks are shown separated by the Abbe resolution limit. Compared to the Rayleigh limit, the decrease in intensity at the origin is much harder to discern. The horizontal line cut in Figure 109D shows that the intensity decreases by only ≈2%.
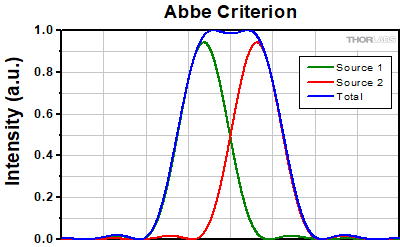 Click to Enlarge
Click to EnlargeFigure 109D The line cut shows the small intensity dip between the two maxima.
 Figure 109C Two point sources separated by the Abbe resolution limit. Though observable, the contrast between the maxima and central minimum is much weaker compared to the Rayleigh limit.
Figure 109C Two point sources separated by the Abbe resolution limit. Though observable, the contrast between the maxima and central minimum is much weaker compared to the Rayleigh limit.Sparrow Criterion
For point source separations corresponding to the Rayleigh and Abbe resolution criteria, the combined intensity profile has a local minimum located at the origin between the two maxima. In a sense, this feature is what allows the two point sources to be resolved. That is to say, if the sources' separation is further decreased beyond the Abbe resolution limit, the two individual maxima will merge into one central maximum and resolving the two individual contributions will no longer be possible. The Sparrow criterion posits that the resolution limit is reached when the crossover from a central minimum to a central maximum occurs.
At the Sparrow resolution limit, the center of the combined intensity profile is flat, which implies that the derivative with respect to position is zero at the origin. However, this first derivative at the origin is always zero, given that it is either a local minimum or maximum of the combined intensity profile (strictly speaking, this is only the case if the sources have equal intensities). Consider then, that because the Sparrow resolution limit occurs when the origin's intensity changes from a local minimum to a maximum, that the second derivative must be changing sign from positive to negative. The Sparrow criterion is thus a condition that is imposed upon the second derivative, namely that the resolution limit occurs when the second derivative is zero [3]. Applying this condition to the combined intensity profile of two Airy disks leads to the Sparrow resolution:
rS = 0.47λ/NA
Figure 109E shows two Airy disks separated by the Sparrow resolution limit. As described above, the intensity is constant in the region between the two peaks and there is no intensity dip at the origin. In the line cut in Figure 109F, the constant intensity near the origin is confirmed.
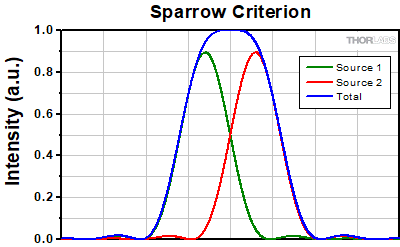 Click to Enlarge
Click to EnlargeFigure 109F At the Sparrow resolution limit, the combined intensity is a constant near the origin. The scale here has been normalized to 1.
 Figure 109E Two Airy disk profiles separated by the Sparrow resolution limit. Note that, unlike the Rayleigh or Abbe limits, there is no decrease in intensity at the origin.
Figure 109E Two Airy disk profiles separated by the Sparrow resolution limit. Note that, unlike the Rayleigh or Abbe limits, there is no decrease in intensity at the origin.References
[1] Eugene Hecht, "Optics," 4th Ed., Addison-Wesley (2002)
[2] S.G. Lipson, H. Lipson, and D.S. Tannhauser, "Optical Physics," 3rd Ed., Cambridge University Press (1995)
[3] C.M. Sparrow, "On Spectroscopic Resolving Power," Astrophys. J. 44, 76-87 (1916)
| Damage Threshold Specifications | |
|---|---|
| Item # | Pulsed Damage Threshold |
| LMUL-10X-UVB | 5.0 J/cm2 at 355 nm, 10 ns, 20 Hz, Ø0.342 mm |
| LMUL-20X-UVB | |
| LMUL-50X-UVB | |
| HPA50XAB | 1.0 J/cm2 at 532 nm, 10 ns, 10 Hz, Ø0.408 mm |
Damage Threshold Data for Thorlabs' Long Working Distance Objectives
The specifications to the right are measured data for Thorlabs' Long Working Distance Objectives.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that shown in Figure 37B represents the testing of one BB1-E02 mirror.

Figure 37A This photograph shows a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
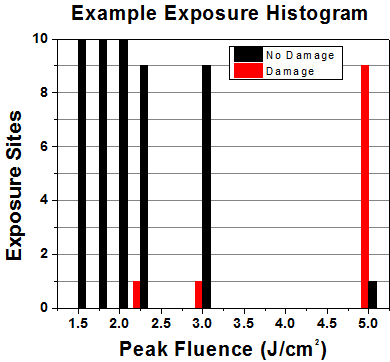
Figure 37B Example Exposure Histogram used to Determine the LIDT of
| Table 37C Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.
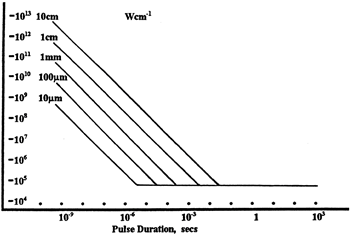
Figure 37D LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
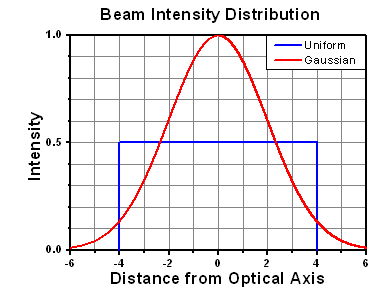
Figure 37E Intensity Distribution of Uniform and Gaussian Beam Profiles
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
- Approximate intensity profile of your beam (e.g., Gaussian)
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated in Figure 37D. Average linear power density can be calculated using this equation.
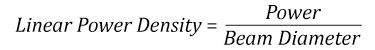
This calculation assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see Figure 37E).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in Table 37F outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Table 37F Laser Induced Damage Regimes | ||||
|---|---|---|---|---|
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
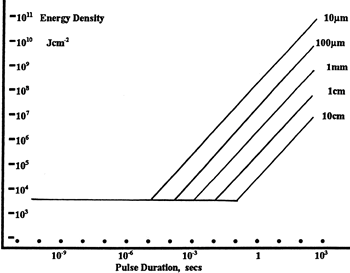
Figure 37G LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. Figure 37G shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
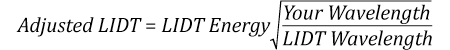
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
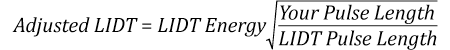
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
In order to illustrate the process of determining whether a given laser system will damage an optic, a number of example calculations of laser induced damage threshold are given below. For assistance with performing similar calculations, we provide a spreadsheet calculator that can be downloaded by clicking the LIDT Calculator button. To use the calculator, enter the specified LIDT value of the optic under consideration and the relevant parameters of your laser system in the green boxes. The spreadsheet will then calculate a linear power density for CW and pulsed systems, as well as an energy density value for pulsed systems. These values are used to calculate adjusted, scaled LIDT values for the optics based on accepted scaling laws. This calculator assumes a Gaussian beam profile, so a correction factor must be introduced for other beam shapes (uniform, etc.). The LIDT scaling laws are determined from empirical relationships; their accuracy is not guaranteed. Remember that absorption by optics or coatings can significantly reduce LIDT in some spectral regions. These LIDT values are not valid for ultrashort pulses less than one nanosecond in duration.

Figure 71A A Gaussian beam profile has about twice the maximum intensity of a uniform beam profile.
CW Laser Example
Suppose that a CW laser system at 1319 nm produces a 0.5 W Gaussian beam that has a 1/e2 diameter of 10 mm. A naive calculation of the average linear power density of this beam would yield a value of 0.5 W/cm, given by the total power divided by the beam diameter:
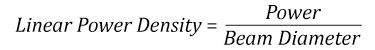
However, the maximum power density of a Gaussian beam is about twice the maximum power density of a uniform beam, as shown in Figure 71A. Therefore, a more accurate determination of the maximum linear power density of the system is 1 W/cm.
An AC127-030-C achromatic doublet lens has a specified CW LIDT of 350 W/cm, as tested at 1550 nm. CW damage threshold values typically scale directly with the wavelength of the laser source, so this yields an adjusted LIDT value:

The adjusted LIDT value of 350 W/cm x (1319 nm / 1550 nm) = 298 W/cm is significantly higher than the calculated maximum linear power density of the laser system, so it would be safe to use this doublet lens for this application.
Pulsed Nanosecond Laser Example: Scaling for Different Pulse Durations
Suppose that a pulsed Nd:YAG laser system is frequency tripled to produce a 10 Hz output, consisting of 2 ns output pulses at 355 nm, each with 1 J of energy, in a Gaussian beam with a 1.9 cm beam diameter (1/e2). The average energy density of each pulse is found by dividing the pulse energy by the beam area:
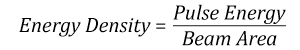
As described above, the maximum energy density of a Gaussian beam is about twice the average energy density. So, the maximum energy density of this beam is ~0.7 J/cm2.
The energy density of the beam can be compared to the LIDT values of 1 J/cm2 and 3.5 J/cm2 for a BB1-E01 broadband dielectric mirror and an NB1-K08 Nd:YAG laser line mirror, respectively. Both of these LIDT values, while measured at 355 nm, were determined with a 10 ns pulsed laser at 10 Hz. Therefore, an adjustment must be applied for the shorter pulse duration of the system under consideration. As described on the previous tab, LIDT values in the nanosecond pulse regime scale with the square root of the laser pulse duration:
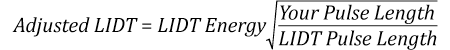
This adjustment factor results in LIDT values of 0.45 J/cm2 for the BB1-E01 broadband mirror and 1.6 J/cm2 for the Nd:YAG laser line mirror, which are to be compared with the 0.7 J/cm2 maximum energy density of the beam. While the broadband mirror would likely be damaged by the laser, the more specialized laser line mirror is appropriate for use with this system.
Pulsed Nanosecond Laser Example: Scaling for Different Wavelengths
Suppose that a pulsed laser system emits 10 ns pulses at 2.5 Hz, each with 100 mJ of energy at 1064 nm in a 16 mm diameter beam (1/e2) that must be attenuated with a neutral density filter. For a Gaussian output, these specifications result in a maximum energy density of 0.1 J/cm2. The damage threshold of an NDUV10A Ø25 mm, OD 1.0, reflective neutral density filter is 0.05 J/cm2 for 10 ns pulses at 355 nm, while the damage threshold of the similar NE10A absorptive filter is 10 J/cm2 for 10 ns pulses at 532 nm. As described on the previous tab, the LIDT value of an optic scales with the square root of the wavelength in the nanosecond pulse regime:
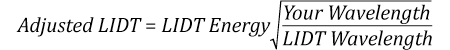
This scaling gives adjusted LIDT values of 0.08 J/cm2 for the reflective filter and 14 J/cm2 for the absorptive filter. In this case, the absorptive filter is the best choice in order to avoid optical damage.
Pulsed Microsecond Laser Example
Consider a laser system that produces 1 µs pulses, each containing 150 µJ of energy at a repetition rate of 50 kHz, resulting in a relatively high duty cycle of 5%. This system falls somewhere between the regimes of CW and pulsed laser induced damage, and could potentially damage an optic by mechanisms associated with either regime. As a result, both CW and pulsed LIDT values must be compared to the properties of the laser system to ensure safe operation.
If this relatively long-pulse laser emits a Gaussian 12.7 mm diameter beam (1/e2) at 980 nm, then the resulting output has a linear power density of 5.9 W/cm and an energy density of 1.2 x 10-4 J/cm2 per pulse. This can be compared to the LIDT values for a WPQ10E-980 polymer zero-order quarter-wave plate, which are 5 W/cm for CW radiation at 810 nm and 5 J/cm2 for a 10 ns pulse at 810 nm. As before, the CW LIDT of the optic scales linearly with the laser wavelength, resulting in an adjusted CW value of 6 W/cm at 980 nm. On the other hand, the pulsed LIDT scales with the square root of the laser wavelength and the square root of the pulse duration, resulting in an adjusted value of 55 J/cm2 for a 1 µs pulse at 980 nm. The pulsed LIDT of the optic is significantly greater than the energy density of the laser pulse, so individual pulses will not damage the wave plate. However, the large average linear power density of the laser system may cause thermal damage to the optic, much like a high-power CW beam.
| Posted Comments: | |
Qian-Qian Zhang
(posted 2024-12-22 11:10:51.807) Could you suggest a holder for this objective? cdolbashian
(posted 2025-01-02 04:55:32.0) Thank you for reaching out to us with this inquiry. After reaching out to you directly, it seems you are interested in adapting this objective into cage system, You can easily do this by using something like SM1A27. The internal threads of which match the objective, while the external-facing threads feature our standard 1" optical threading: SM1. user
(posted 2024-11-21 12:30:10.34) It is not clear what camera can be used with these objectives. For Mitutoyo, the OFN is 24 (ie 24mm diagonal image, used with the nominal 200mm lens tube), but they specify FOV only with a 1/2'' sensor (8mm diagonal) and 24mm eyepiece (OFN 24-> 24mm diagonal).
Assuming the difference is just to cater to the higher sharpness of the sensor, and vignetting is probably not visible in the eyepiece case by design : would we be able to use a 24mm diagonal sensor (max), at the cost of some loss of sharpness in the edges ? (that the eye doesn't resolve in the eyepiece case) srydberg
(posted 2024-11-28 04:22:53.0) Hi, thank you for your question! We have contacted you to discuss your application. user
(posted 2024-04-16 17:47:10.7) I would use the Mitutoyo Apochromatic NIR Objectives to focus my laser light.
My laser have Gaussian beams with very nice modes.
How well I can focus with these objectives, any information on that?
We usually need a beam that is 2um spot size, to properly image our samples. I would be interested in estimate of beam spot sizes for 400nm, 800 nm and 1500nm? Of course assuming some input beam spot diameter from the laser itself.
Do you have any information on this matter? user
(posted 2024-03-22 11:27:17.213) Is this objective compatible with this zoom lens (https://www.thorlabs.com/thorproduct.cfm?partnumber=MVL6X3Z)?
For context, we would like to build a microscope camera system that is able to image micrometer features on chips. cdolbashian
(posted 2024-03-29 02:16:45.0) Thank you for reaching out to us with this inquiry! The zoom lenses we carry are not meant to directly be compatible with a objective lens, as the objective adds an afocal lens element into the zoom lens system which has a known front and rear focal length. That being said, I potentially have some suggestions for you, which I have emailed you directly to discuss. Derrek Wilson
(posted 2023-10-11 09:38:43.997) hello,
For the NIR objectives, the Magnification is given this condition:
When Used with a 200 mm Focal Length Tube Lens
Could Thorlabs suggest a product that satisfies this requirement for a c-mount camera? seongjun park
(posted 2023-02-20 23:32:35.9) We are planing to develop a inspection system using this objective lens (MY10X-803).
Would it be possible to get zemax blackbox model of this item?
Best,
Seongjun Park cdolbashian
(posted 2023-04-03 12:10:59.0) Thank you for reaching out to us with this inquiry. While we would love to assist in this manner we unfortunately cannot. This is a Mitutoyo component and we do not have access to their simulation data/files. Marina Servol
(posted 2022-09-29 16:19:59.827) Hello,
I've seen you sell kinematics mounts for RMS thread but I would like to use a Mitutoyo objective. Do you have any adaptater or idea in order I can attach my objective to a mount ?
Thanks for your response,
Marina Servol cdolbashian
(posted 2022-10-04 04:10:57.0) Thank you for reaching out with your inquiry. Looking at the threading on our Mitutoyo objectives, it seems like you would need an adapter which converts the M26x0.706 threads to our standard 1" optical threading of our SM1 thread. In this case, you would likely want the SM1A27. All of our adapters can be found at this convenient location: https://www.thorlabs.com/navigation.cfm?guide_id=2327 Sapun Parekh
(posted 2022-06-09 18:14:46.177) Hello,
I think this is a great product and have a few question for potential customization.
Can you make this AR-coated all the way into the IR say 1700 nm?
Also, I would like to see the theoretical axial color aberration until 1700 nm. Can you provide the data?
Thanks,
Sapun Parekh cdolbashian
(posted 2022-06-21 11:03:44.0) Thank you for reaching out to us Sapun. I have contacted you to discuss this potential custom. Additionally, we do not have data up until 1700nm, but have shared extended IR data until 1300nm. user
(posted 2022-05-13 06:54:07.477) Do you know the maximum power density (energy) permissible i.e. damage threshold for nanosecond pulses with the Mitutoyo NIR objectives? cdolbashian
(posted 2022-06-17 04:32:31.0) Thank you for your inquiry here. Unfortunately we do not have damage threshold data for this for an arbitrary pulsed laser. For more specific information, I recommend reaching out to the vendor. Wu Wei
(posted 2022-03-24 09:22:46.943) ZAR black box? cdolbashian
(posted 2022-03-25 11:52:43.0) Thank you for reaching out to us with this request. You are specifically inquiring after a black box of a Mitutoyo objective. Unfortunately, as the vendor considers them proprietary, they do not share the ZAR files with us. Raj Kumar
(posted 2022-03-09 19:25:08.157) Hello Thorlabs support team,
I would like to couple light of broad spectral range 450 to 650 nm in to a single mode fiber (SM405XP) without introducing any chromatic aberration. What do you suggest (solutions other than fiber port couplers)?. I was looking for Mitutoyo apochromatic objectives but I could not find the information of axial focal shift with respect to wavelength. cdolbashian
(posted 2022-03-25 03:11:43.0) Thank you for contacting us Raj. For broadband applications, the reflective parabolic mirrors are ideal due to the chromatic insensitivity of the reflection. That being said, alignment of a reflective coupler/collimator is highly nontrivial when used to couple into a fiber. Regarding the Mitutoyo objective, unfortunately, we do not have axial focal shift data. If you are interested in an objective with such data provided, I suggest you look at some of the thorlabs-brand objectives, as we provide ample documentation, as well as ZAR files for simulation. nimrod nissim
(posted 2021-11-28 08:02:10.91) missing Zemax BB file YLohia
(posted 2021-11-29 03:44:57.0) Thank you for contacting Thorlabs. Unfortunately, Mitutoyo does not provide us with Zemax files for their objectives. james hale
(posted 2021-11-09 17:09:56.353) Hello,
We have installed this objective into a re entrant viewport which allows it to focus inside of a small UHV vacuum system. We are needing to bake that system here shortly. The objective is also mounted onto a linear stage which can better help focus into the center of our chamber, and when backed out of the chamber as far as possible, only ~1" of the objective remains inside of the re entrant viewport.
While the objective itself is not in direct contact with any part of the vacuum system, and it is surrounded by a 10mm air gap on all sides which is open to atmosphere, we still fear that the heat from the chamber itself (baked to 150c for 24 hours), may in turn heat this microscope objective too.
I have been unable to find anything regarding the maximum heat for using or storing this microscope objective, and am trying to find those values if they exist. I assume that the optically bonded elements inside the objective will not take well to being heated above normal room temperature...
We can of course remove the objective entirely and heat our system with no fear of heating the objective, but this would unfortunately lead to a loss of a very precise and lengthy alignment process which has been accomplished.
Any help or advice concerning the possible heating of this objective would be much appreciated. Thank you. jgreschler
(posted 2021-11-10 02:11:40.0) Thank you for contacting Thorlabs. The recommended temperature range from Mitutoyo who manufactures this objective is 5 to 45 deg C. I have contacted you directly to discuss this further. Verena Buehler
(posted 2020-08-14 11:39:42.21) Hello Thorlabs Team,
I was wondering why you do not offer a black box file for this popular Objective?
It would be helpful to simulate in Zemax how or if a individual setup works with it.
Please contact me for any helpful information.
Kind regards,
Verena Buehler nbayconich
(posted 2020-08-17 10:10:52.0) Thank you for your feedback. Our vendor Mitutoyo unfortunately does not provide us with zemax models for these objectives. I will reach out to you directly to discuss your application. Shankar MENON
(posted 2020-06-22 17:43:38.59) Is it possible to get objective AR coated for high transmission at a specific wavelength? YLohia
(posted 2020-06-23 09:22:58.0) Hello, thank you for contacting Thorlabs. Custom optics can be requested by emailing techsupport@thorlabs.com. We will reach out to you directly to discuss the possibility of offering this. user
(posted 2020-04-07 10:43:42.103) Concerning Mitutoyo NIR objectives, do you have any info how much the focal length changes (e.g. at 1550 [nm]) respective to the visible range? It would typically be helpful to know if it is more or less than the Rayleigh range. llamb
(posted 2020-04-13 09:54:47.0) Thank you for your feedback. The focal shift can be up to 15 µm for wavelengths in the 1100-1600 nm range. More detailed information could be provided after discussing your application further. I see that your contact information was not provided, so feel free to reach out to techsupport@thorlabs.com if you would like further information. Clara Rittmann
(posted 2019-10-17 10:12:14.72) Hi, I do not understand why the effective focal length can be significantly smaller than the working distance at the long distance working objectives such as the MY50x-825. How is that achieved? I just do not feel comfortable about using optics that I do not fully understand.
Thanks! YLohia
(posted 2019-10-17 11:30:33.0) Hello Clara, the EFL is defined as the distance between the principal plane and the focus spot, in order provide users a number to perform calculations for field of view, focused spot size, etc. The principle plane does not necessarily have to be within the length of the objective itself and, in this case, is specifically designed to be outside of it in order to achieve a long working distance. user
(posted 2019-02-03 23:59:26.797) Have you considered, as e.g. order on demand item, also to supply the rest of the Mitutoyo Plan App line e.g. the HR Plan Apo series. nbayconich
(posted 2019-02-06 03:29:34.0) Thank you for contacting Thorlabs. At the moment we do not have plans to release additional Mitutoyo objectives but we can provide special orders upon request. Please contact techsupport@thorlabs.com regarding any special order requests. np
(posted 2018-03-26 20:46:08.447) Can you please tell what is the location of the back focal plane of the MY100X-806 relative to the end of the lens? nbayconich
(posted 2018-03-31 03:51:36.0) Thank you for contacting Thorlabs. Information such as the back focal plane location is typically proprietary for most objective lens manufacturers and can only provide certain specifications to particular end users. I will reach out to you directly to discuss your application and provide more information if possible. maciej.koperski
(posted 2017-10-04 11:50:15.6) Dear Sir/Madam
Could you please provide information, in which spectral range can this objective be used? Could you perhaps show transmission spectra?
With best regards,
Maciej Koperski nbayconich
(posted 2017-10-12 10:36:40.0) Thank you for contacting Thorlabs. Mitutoyo's objective transmission spectrum is proprietary information. The recommended performance range for these objectives is between 450nm - 650nm. I will reach out to you directly. |

- AR Coated for 240 - 360 nm
- Ideal for Laser Focusing and UV Imaging Applications
- Diffraction-Limited Performance
- 10X, 20X, or 50X Magnification
Thorlabs MicroSpot objectives provide long working distances while keeping axial focal shift low. Their optical design is chromatically optimized in the UV wavelength range. Diffraction-limited performance is guaranteed over the entire clear aperture. These objectives are ideal for laser cutting, surgical laser focusing, and spectrometry applications. They can also be used for scanning and micro-imaging applications like brightfield imaging under narrowband, UV laser illumination. Each objective is shipped in an objective case comprised of an OC2M26 lid and an OC24 canister.
Each objective is engraved with its class, magnification, numerical aperture, wavelength range, a zero (noting that it is to be used to image a sample without a cover glass), and optical field number. For an explanation of the defining properties of these objectives, please see the Objective Tutorial tab.
Thorlabs can provide these objectives with custom AR coatings on request by contacting Tech Support; options include broadband NUV (325 nm - 500 nm), dual band (266 and 532 nm), and laser line (248 nm, 266 nm, 355 nm, or 532 nm). We also offer additional MicroSpot objectives for laser-focusing applications in the UV as well as visible and near-IR wavelengths.
| Item # | AR Coating Wavelength Range |
Ma | WD | EFL | NA | EPb | Resolutionc | Typical Transmission | OFN | PFL | AR Coating Reflectanced |
Pulsed Damage Threshold |
Objective Threading |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LMUL-10X-UVB | 240 - 360 nm | 10X | 20.0 mm | 20 mm | 0.25 | 10.0 mm | 0.9 µm | Raw Data |
24 | 95.0 mm | (240 - 360 nm) |
5.0 J/cm2 (355 nm, 10 ns, 20 Hz, Ø0.342 mm) |
W26 x 0.706; 5 mm Depth |
| LMUL-20X-UVB | 20X | 15.3 mm | 10 mm | 0.36 | 7.2 mm | 0.6 µm | Raw Data |
||||||
| LMUL-50X-UVB | 50X | 12.0 mm | 4 mm | 0.42 | 3.4 mm | 0.5 µm | Raw Data |

- AR-Coated for 400 - 1100 nm
- Axial Color Corrected for 436 - 850 nm
- Ideal for Laser Focusing; Brightfield, Darkfield, and Fluorescence Microscopy; and Two-Photon Imaging
- 50X Magnification
Thorlabs offers a High-Resolution Plan Apochromatic Improved Visible (APO VIS+) Microscope Objective for 400 to 1100 nm that provides axial color correction over a wide field of view with no vignetting over the entire field. Compared to common apochromatic microscope objectives, which are typically axial color corrected from the 436 nm (g-line) to 656 nm (C-line), our PLAN APO VIS+ objective has an extended corrected wavelength range from 436 nm (g-line) to 850 nm. The objective is designed for use with a tube lens focal length of 200 mm and has optical elements that are AR-coated for improved transmission between 400 nm and 1100 nm. For more details on these objectives, please click the info icon (![]() ) below. Our 50X objective has a high numerical aperture (NA) of 0.75, making it ideal for applications requiring high-resolution such as laser focusing; brightfield, darkfield, and fluorescence microscopy; and two-photon imaging. Each objective is shipped in an objective case comprised of an OC2M26 lid and an OC24 canister.
) below. Our 50X objective has a high numerical aperture (NA) of 0.75, making it ideal for applications requiring high-resolution such as laser focusing; brightfield, darkfield, and fluorescence microscopy; and two-photon imaging. Each objective is shipped in an objective case comprised of an OC2M26 lid and an OC24 canister.
We also offer a 15X APO VIS+ objective, TL15X-2P, that is optimized for multiphoton imaging and features a lockable correction collar that allows adjustment for spherical aberrations introduced by imaging through aqueous solutions or cover glasses up to 2.8 mm thick.
This objective is engraved with its class, magnification, numerical aperture, a zero (noting that it is to be used to image a sample without a cover glass), and optical field number. For an explanation of the defining properties of this objective, please see the Objective Tutorial tab.

- For Use from 436 nm to 656 nm
- Suitable for Brightfield Microscopy
- 5X, 7.5X, 10X, 20X, 50X, or 100X Magnification
Thorlabs offers Mitutoyo Plan Apochromat Objectives with 5X, 7.5X, 10X, 20X, 50X, or 100X magnification. They feature a flat field of focus and chromatic correction in the visible range. The long working distance provides a wide space between the lens surface and the object, making them ideal for machine vision applications. Each objective is engraved with its class, magnification, numerical aperture, a zero (noting that it is to be used to image a sample without a cover glass), and the tube lens focal length for which the specified magnification is valid. For an explanation of the defining properties of these objectives, please see the Objective Tutorial tab. If the case shipped with each of these objectives is lost or broken, Thorlabs offers an objective case (Item #s OC2M26 and OC24) that can be used as a replacement.

- For Use from 480 nm to 1800 nm
- Suitable for Brightfield Microscopy and Laser Focusing
- 5X, 10X, 20X, or 50X Magnification
Thorlabs offers Mitutoyo Plan Apochromat Near-Infrared (NIR) Objectives with 5X, 10X, 20X, or 50X magnification. They feature a flat field of focus and chromatic correction in the visible range with extended transmission to 1800 nm. The long working distance provides a wide space making them ideal for machine vision applications or laser focusing. Each objective is engraved with its class, magnification, numerical aperture, a zero (noting that it is to be used to image a sample without a cover glass), and the tube lens focal length for which the specified magnification is valid. For an explanation of the defining properties of these objectives, please see the Objective Tutorial tab. If the case shipped with each of these objectives is lost or broken, Thorlabs offers an objective case (item #s OC2M26 and OC24) that can be used as a replacement.
 Products Home
Products Home


















 Zoom
Zoom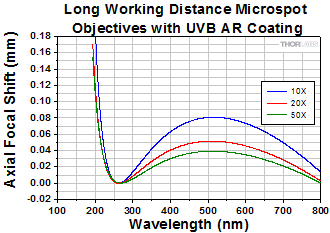



 Long Working Distance Objectives
Long Working Distance Objectives